|
Calculus is traditionally taught in either the Senior year in high school or the Freshman year in college. It was discovered by Isaac Newton and, independently, Gottfried Leibniz before 1700. Usually, the course starts with the differential side of calculus, but I've chosen start with the integral side. I believe it makes for a little more intuitive presentation.
If you can remember some of your high school algebra and trigonometry then the discussion below will be understandable. While the discussion below is accurate, it is not rigorous from a mathematical point of view. For a very rigorous presentation see Tom Apostle's book; and for a somewhat less rigorous, but more complete presentation see Mike Spivak's book. In the discussion below you will see all the major ideas from Calculus, and (I hope) you will gain enough understanding to comprehend how they can be applied in areas like basic circuit theory or electromagetic waves. There are no exercises or examples here, so if you wish to gain skills in the actual computational aspects of calculus you will have to work through a book like the one by Frank Ayres.
Let's look at a landscaping problem to view a Calculus technique in a (semi) real life situation. Suppose that you want to make a patio/walkway using pavers in a shape like this:

This patio provides a straight walkway with a couple of sitting areas off to one side. How many pavers do you need to buy? Let's say you're going to use square pavers. You could draw the area on graph paper scaling so that one grid square represents one paver. Then you count up the number of grid squares needed to cover the walkway and you'll have enough. You might be able to use a few less because not all of them are full pavers. We'd say this gives you an "upper bound" on the number of pavers you need. You could get a "lower bound" by counting the squares inside your drawing. If you used smaller pavers, would the corresponding upper and lower bounds be closer to the actual area of the walkway? Intuition says yes. Imagine using smaller and smaller pavers ... the upper and lower bounds will get closer and closer together and you'd be able to get almost exactly the correct number. If you knew the size of each paver, you could calculate a very close approximation to the size of the area of your patio
You just learned the hardest part of Integral Calculus!
Consider a function f(x) that produces a graph like:
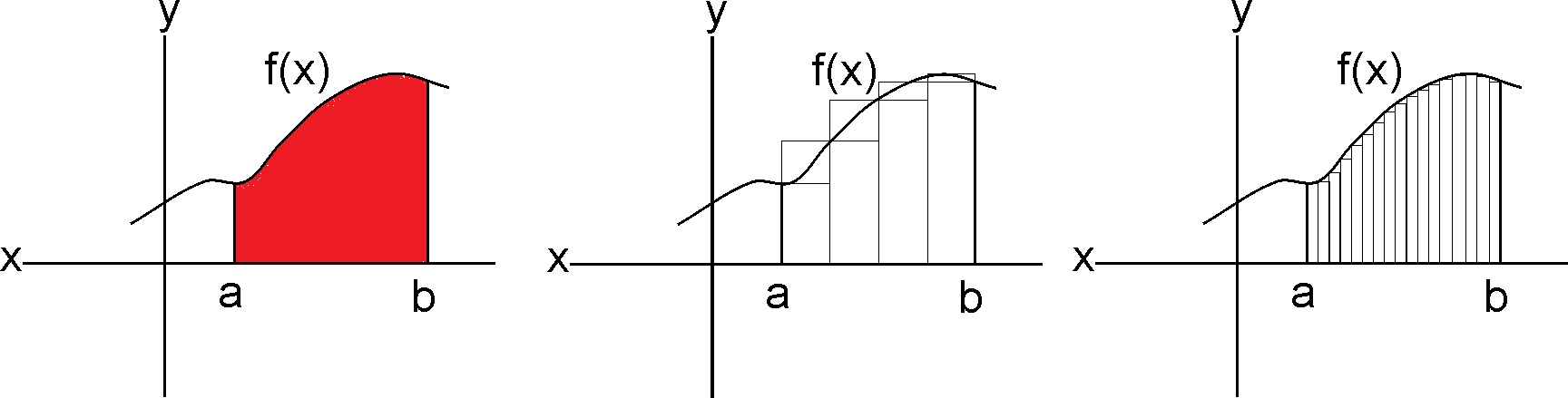
The problem considered by Integral Calculus is to find the area of the shape bounded by the graph of f(x), the x-axis and the vertical lines at x=a and x=b (the area shown in red). The problem is pretty much like finding the number of pavers needed above, and we use almost the same technique to do it.
Draw rectangles of equal width so that they cover the shape in question, they form an upper bound for the area. Then draw rectangles so that they fit inside the shape to form the lower bound for the area. It is easy to calculate the area of each rectangle and add them together to get upper and lower bounds for the area of our shape. If we make the width of the rectangles smaller and smaller, the upper and lower bounds get closer and closer together and will eventually "converge" to the area of the shape. To be completely honest, there are functions for which they don't converge, but we won't encounter any of those here.
If we can find what that convergence value is, we've solved the problem. In formal notation we write:
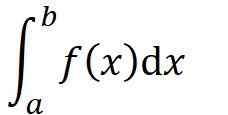
The area of the shape is "the definite integral of the function f(x) from the point a to the point b".
In a formal setting there are conditions placed on all of this, but for practical purposes that's it. Calculating that convergence point might be quite difficult by hand, but in this day of computers it's (usually) pretty easy.
Sometimes one can find a function F(x) related to f(x) so that:
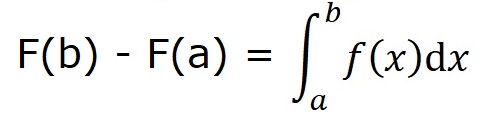
We call such an F(x) an "Indefinite Integral" for f(x). When we are only hopeful that there is such a function we use the notation:
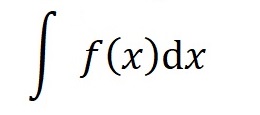
We'll find out more about these indefinite integrals after we learn about differential calculus.
Before we move on, there is a notion that we should look at. Integrals are "additive". It's pretty intuitive when you look at the picture:
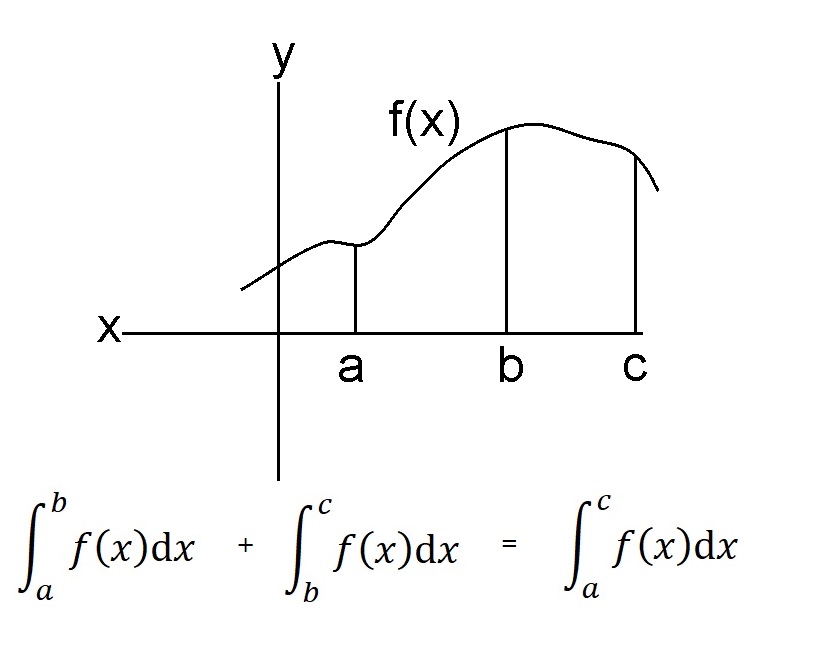
We'll come back to integrals in a bit, but we first need to understand the other big part of the story and that is Differential Calculus. The problem here is to look at a graph like the one above and at any point find the straight line that best approximates the graph. The reason for doing that is because straight lines are really easy to work with. Such an approximation is only good for a small area around the point in question, but the ideas can be extended to an amazing degree.
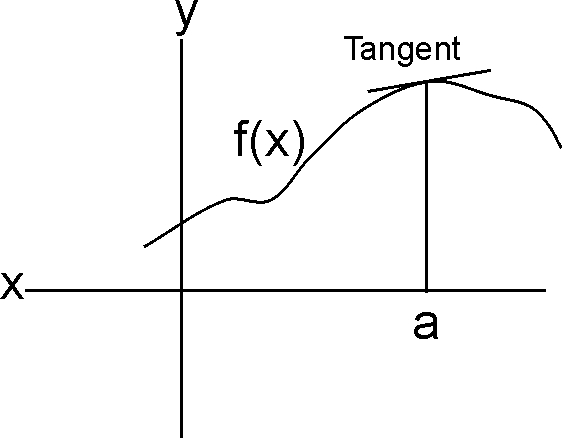
So, how do we find that straight line (also known as a tangent line)? We know that two points determine a straight line - you've done it many times with ruler and two marks. We already have one point (a, f(a)), so pick a point nearby and try that (a+h, f(a+h)). Note: we used several small negative values for "h" in the picture below.
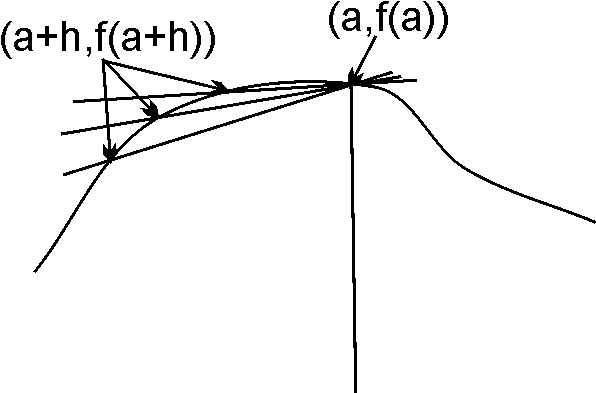
If we make h smaller and smaller then the corresponding line gets closer and closer to our desired tangent line. Since it is awkward to consider the limit of a bunch of lines we just look at the slope of the line (which is a number) and we can say the slope of the tangent line to the curve at point x is:
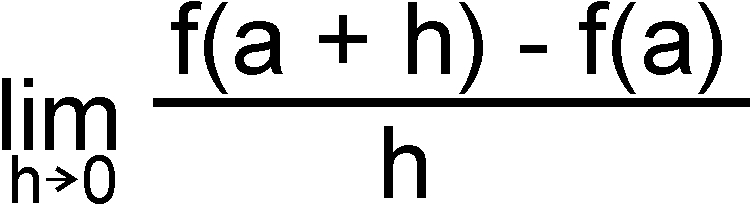
If we can do this generically (eg for any x replacing a) then we call the resulting function the "derivative" of f(x) and denote it by f'(x) or df/dx.
Calculating these things can be a bit difficult, but it turns out there are some mechanisms that don't require figuring out the limits all the time. I'll cover some of those rules further along in this discussion, along with similar methods for integrals.
Before we do that, we need to cover the punch line that displays the relationship between integral and differential calculus.
This theorem says that if you have a function F(x) whose derivative is f(x), then F(x) is an indefinite integral for f(x). Sound like double talk? It comes out better if we say:
if F'(x) = f(x) then:
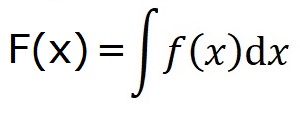
This needs some explanation. For a full proof of the theorem see Tom Apostle's book. Wikipedia has several excellent and intuitive explanations here.
The "rules" listed below are relatively easy to derive from the basic definitions. See any of the books in the references for a full explanation. For our puposes we'll just acept them as true. In order to really understand them you'll probably have to look at some examples - I recommend the Frank Ayres book.
g(x) = cf(x) where c is a constant then g'(x) = cf'(x).
g(x) = f(x) + h(x) then g'(x) = f'(x) + h'(x)
g(x) = f(x)h(x) then g'(x) = f(x)h'(x) + f'(x)h(x)
g(x) = f(h(x)) then g'(x) = f'(h(x))h'(x) this is called the chain rule.
Similarly, we have a list of rules that are helpful in finding indefinite integrals.
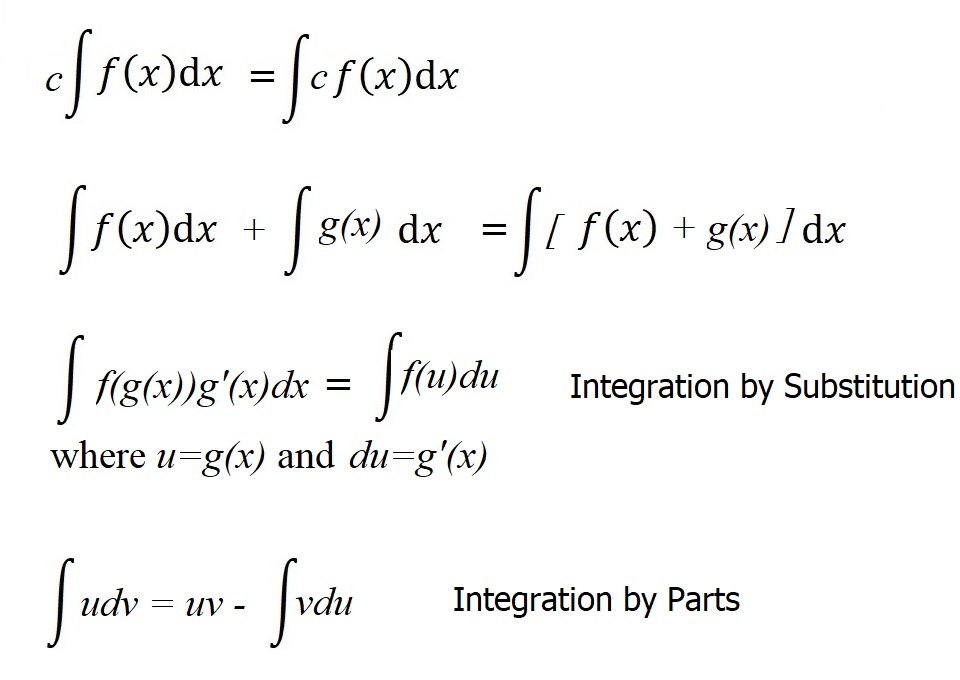
There are a few functions that we normally deal with. These appear in nature over and over again. These are generally trigonometric functions, logarithmic/exponential functions, polynomials. Below are the basic functions and their graphs:
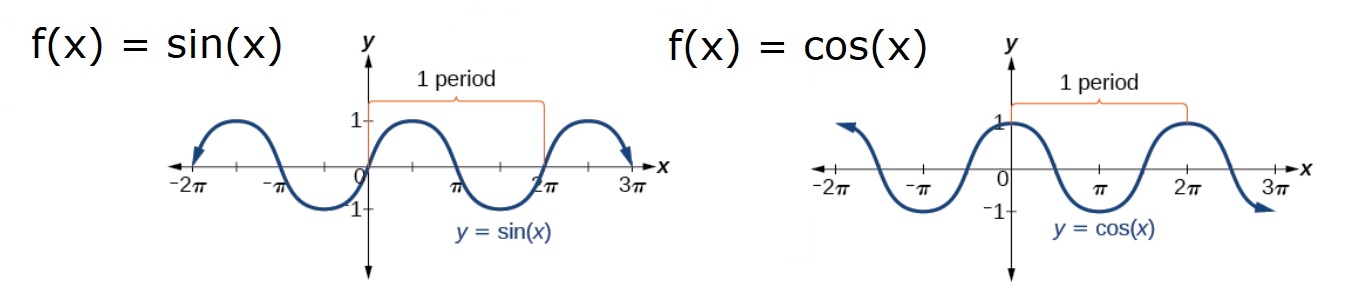
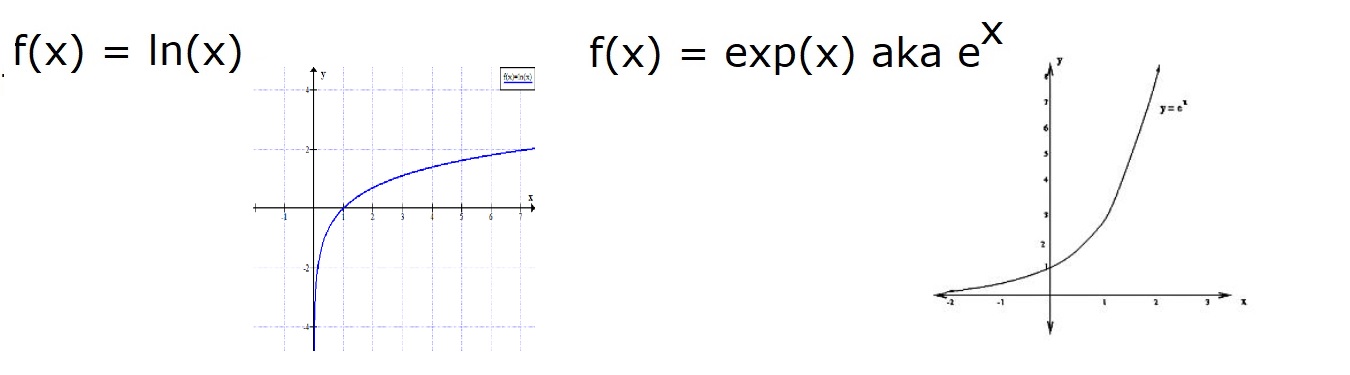
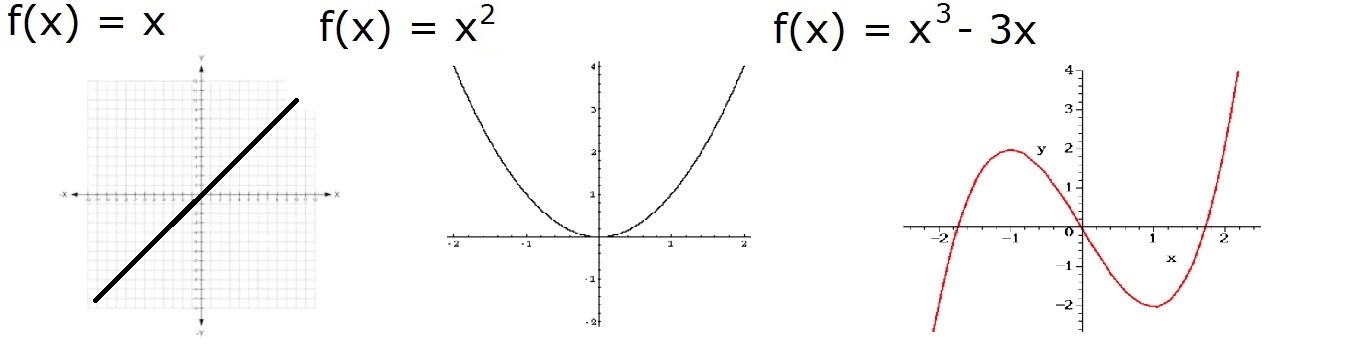
After some work one can show the derivatives of these functions are:
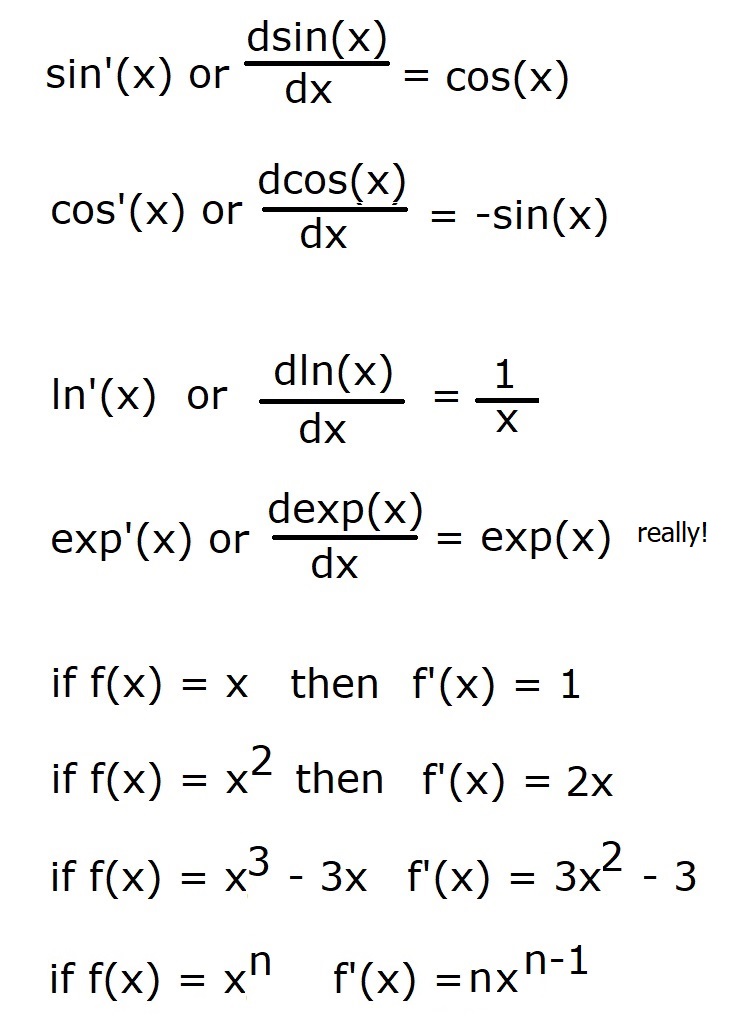
With this set of known derivatives and the rules for derivatives of combined functions we can calculate most of the derivatives we might encounter in real world applications. We can also calculate most of the integrals we will find in real applications such as electronics and physics. Getting good at these things is what consumes most of the time in a regular calculus course. I recommend digging into the Frank Ayres book to gain that proficiency.
There are many places where these ideas are used. Economics, statistics, physics, mechanical engineering, chemistry.... I'm hoping to work on applications to basic circuit theory in a sequal to this paper.
For now, most of us know Ohm's law which shows the relationship between voltage, current and resistance. This is a "time invariant" formula, so that if you have a voltmeter across the resistor and apply the voltage, nothing changes over time. The same is NOT true for inductors and capacitors. In fact, the relationships are:
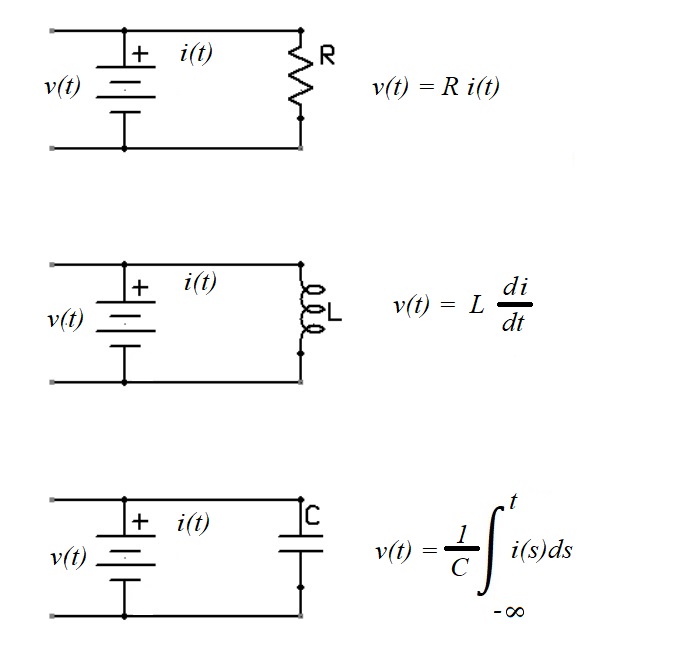
Let's end this discussion on that cliff hanger!
The few references below cover most of what one could want about these topics. There are dozens of alternative materials which you can find by searching for calculus on Amazon.